18.2 Analytische Geometrie
Die folgende Aufgabe stammt aus „Elemente der Mathematik, Leistungskurs Lineare
Algebra / Analytische Geometrie“, Westermann Schroedel Diesterweg, Braunschweig 2004,
S. 228:
Gegeben sind die Ebene E und die Geradenschar gp mit p 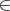
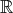 .
.
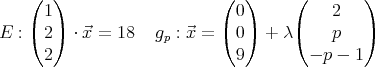
- Gib eine Gleichung der Kugel um den Punkt P(2|1|2) an, welche die Ebene E berührt,
und berechne den Berührungspunkt.
- Zeige, dass für alle p gilt: gp liegt in E.
- Welche Geraden sind Tangenten der Kugel aus Teilaufgabe a) ?
18.2.1 Lösung mit Archimedes
-
- Eingabe der Ebenengleichung über „Typische Aufgaben - Ebene - Koordinatenform“.
Hierfür muss man natürlich wissen, dass die gegebene Form der Koordinatenform
x + 2y + 2z = 18 entspricht.
- Eingabe des Punktes durch Doppelrechtsklick, anschließend Rechtsklick auf den
Punkt und Eingabe der Koordinaten
- Fällen des Lotes von P auf E, Benennen des Lotfußpunktes mit L.
- Messen des Abstandes von P zum Lotfußpunkt, z.B. über Makros - Abstände - Punkt
Punkt.
- Einzeichnen der Kugel durch Markieren von P und L.
Die Kugel hat also die Gleichung 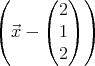 2 =
2 =  2.
2.
- Die Aussage kann mit Archimedes natürlich nur überprüft, aber nicht bewiesen werden.
- Erzeuge einen Schieberegler mit Extras - Schieberegler, nenne ihn z.B. „pp“ (denn P
ist schon vergeben, es darf kein zweites Objekt mit diesem Namen geben, auch wenn
er klein statt groß geschrieben wird).
- Gib die Geradengleichung unter „typische Aufgaben - Gerade in Parameterform“ mit
dem Parameter pp so ein, wie sie in der Aufgabenstellung steht, ersetze dabei lediglich
„p“ durch „pp“. Markiere dabei die Einstellungsbox „Ausdruck enthält Terme“.
- Wenn man nun am Schieberegler den Parameter p variiert, so sieht man, dass sich
die Gerade immer auf E bewegt.
- Hier kann man z.B. durch Probieren feststellen, dass der gesuchte Parameter 2 ist, oder die
Gerade einfach konstruieren (nach dem Parameter ist ja nicht gefragt) und die Form dann durch
Rechtsklick - Beschreibung ablesen.
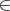
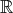 .
.
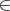
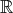 .
.
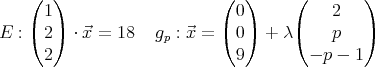
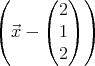 2 =
2 =  2.
2.